08：00-24:00
(2013年海淀高三期末)已知正方体的棱长为，动点在正方体表面上运动，且()．记点的轨迹的长度为．
(1) 求
；
(2) 求出关于的方程的解的个数的所有可能的值，并说明理由．
分析与解由于正方体绕其体对角线旋转后仍与自身重合，于是为点在正方体的侧面与上的轨迹长度之和的倍．将右侧面翻折至与侧面重合，如图．稍加探索可以发现和是两个分界点．
(1) 当时，有
，于是
．
(2) 当时，图中弧的半径为，所对的圆心角为
记
，其中
，则对应的弧长
其导函数
于是随着的增大，随之增大，对应的弧长随之减小，随之减小．
当时，设
，其中
，则弧长之和
于是
设
则
，
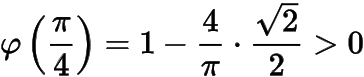
，而
因此在
上先负后正，对应的在
先递减再递增．
这样我们就可以勾勒出函数的图象如下．
于是方程的解的个数的所有可能值为．
注本题是北京海淀区高三期末考试的一道填空题，为了严格地说清为什么解的个数有且只有这些很需要费一番功夫．
根据学生的高考分数、意向专业 为您查找适合你的院校列表， 24小时内短信电话发送给你！
